MATHS 2 PAPER

DOWNLOAD MATHEMATICS 2 - MATHS 2 PREVIOUS YEARS QUESTION PAPERS B.TECH PTU FIRST YEAR

AMA-102 MATHEMATICS-2
(B.Tech 1st & 2nd Semester,2063)
Time : 3 Hours
Maximum Marks : 60

NOTE:- This paper consist of Three Sections. Section A is compulsory. Answer any Four questions from Section B and C, selecting at least Two questions from each section.

Section-A Marks : 20

1(a) Find the rank of the matrix :



(b) Prove that (1/r) = 0, where r is the distance of a variable point P from the origin.
(c) State Guass-Divergence theorm.
(d) If the probability of male birth is 0.5, find the probability that in a family of 4 children there will be atleast one boy.
(e) State Student's t-test.
(f) If P and Q are functions of x, write the complete solution of the differential equation, (dy/dx) + Py = Q.
(g) Write the particular integral of (D2 - 2D + 4)y = exsin x.
(h) State Lagrange's interpolation formulla for unequal intervals.
(i) Show that the Matrix :

(j) From the differential equation from y = ex (A cos x + B sin x).




Section-B Marks:8 Each

2. Determine the characteristics roots and the corresponding characteristics vectors of the Matrix :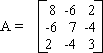


3. (a) Prove that curl(curl V) = grad div V - 2V.
(b) Vector field is given by F = (sin y)i + x(1 + cos y)j
Evaluate the line integral over the circular path given by x2 + y2 = a2, z = 0.


4. Verify Stokes' theorem for the vector field F = (2x - y)i - yz2 - y2zk. over the upper half surface of x2 + y2 + z2 = 1. bounded by its projection on the xy-plane.


5. (a) Find the mean and standard deviation of a normal distribution, when 8% of the items are over 64 and 31 % are under 45. [P (0< z < .496) = 0.19, and P (0 < z < 1 = 0.42]. (b) Fit a Bononial distribution to the following data:

x f
0 28
1 62
2 46
3 10
4 4





Section-C Marks : 8 Each


6. (a) A coin is tossed 400 times, which turns up head 219 times. Do the data justify the hypothesis of an unbiased coin?
(b) In one sample of 8 observations the sum of the squares of the deviations of sample values from the sample mean was 84.4 and in other sample of 10 observations it was 102.6. Test whether this difference is significant at 5% level, given that F.05(7, 9) = 3.29.


7. (a) Solve:

(b) Solve: cos (x + y) dy = dx.



8. (a) Solve (D3 + 3D2 + D)y = x2e2x + sin2x.
(b) Solve:


9. (a) From the following table, estimate the number of students who obtained merks between 40 and 45:
Marks No.of Students
30-40 31
40-50 42
50-60 51
60-70 35
70-80 31

(b) Given the values :
x f(x)
5 150
7 392
11 1452
13 2366
17 5202
Evaluate f(9) using Newton's divided difference formula.